Lexical analysis with lex

Operators

Unlike orange above, most of the expressions that we want to search for cannot be specified so easily. The expression itself might simply be too long. More commonly, the class of desired expressions is too large; it may, in fact, be infinite. Thanks to the use of operators -- summarized in 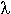GREEK SMALL LETTER LAMBDA O below -- we can form regular expressions to signify any expression of a certain class. The + operator, for instance, means one or more occurrences of the preceding expression, the ? means 0 or 1 occurrence(s) of the preceding expression (which is equivalent, of course, to saying that the preceding expression is optional), and means 0 or more occurrences of the preceding expression. (It may at first seem odd to speak of 0 occurrences of an expression and to need an operator to capture the idea, but it is often quite helpful. We will see an example in a moment.) So m+ is a regular expression that matches any string of ms:

   mmm
   m
   mmmmm

and 7 is a regular expression that matches any string of zero or more 7s:

77 77777

777

The empty third line matches because it has no 7s in it at all.

The | operator indicates alternation, so that ab|cd matches either ab or cd. The operators {} specify repetition, so that a{1,5} looks for 1 to 5 occurrences of a. Brackets, [], indicate any one character from the string of characters specified between the brackets. Thus, [dgka] matches a single d, g, k, or a. Note that the characters between brackets must be adjacent, without spaces or punctuation. The ^ operator, when it appears as the first character after the left bracket, indicates all characters in the standard set except those specified between the brackets. (Note that |, {}, and ^ may serve other purposes as well; see below.) Ranges within a standard alphabetic or numeric order (A through Z, a through z, 0 through 9) are specified with a hyphen. [a-z], for instance, indicates any lowercase letter. Somewhat more interestingly,

   [A-Za-z0-9&#]

is a regular expression that matches any letter (whether upper or lowercase), any digit, an asterisk, an ampersand, or a sharp character. Given the input text

   $$$$?? ????!!!$$ $$$$$$&+====r~~# ((

the lexical analyzer with the previous specification in one of its rules will recognize , &, r, and #, perform on each recognition whatever action the rule specifies (we have not indicated an action here), and print out the rest of the text as it stands. If you want to include the hyphen character in the class, it should appear as the first or last character in the brackets: [-A-Z] or [A-Z-].

The operators become especially powerful in combination. For example, the regular expression to recognize an identifier in many programming languages is

   [a-zA-Z][0-9a-zA-Z]

An identifier in these languages is defined to be a letter followed by zero or more letters or digits, and that is just what the regular expression says. The first pair of brackets matches any letter. The second, if it were not followed by a , would match any digit or letter. The two pairs of brackets with their enclosed characters would then match any letter followed by a digit or a letter. But with the , the example matches any letter followed by any number of letters or digits. In particular, it would recognize the following as identifiers:

   e
   not
   idenTIFIER
   pH
   EngineNo99
   R2D2

Note that it would not recognize the following as identifiers:

   not_idenTIFIER
   5times
   $hello

because not_idenTIFIER has an embedded underscore; 5times starts with a digit, not a letter; and $hello starts with a special character.

A potential problem with operator characters is how we can specify them as characters to look for in a search pattern. The last example, for instance, will not recognize text with a in it. lex solves the problem in one of two ways: an operator character preceded by a backslash, or characters (except backslash) enclosed in double quotation marks, are taken literally, that is, as part of the text to be searched for. To use the backslash method to recognize, say, a followed by any number of digits, we can use the pattern

   \[1-9]

To recognize a \ itself, we need two backslashes: \\. Similarly, ``"x\

x"'' matches xx, and ``"y\"z"'' matches y"z. Other lex operators are noted as they arise in the discussion below. lex recognizes all the C language escape sequences.

lex operators

Expression Description

\x x, if x is a lex operator

"xy" xy, even if x or y are lex operators (except \)

[xy] x or y

[x-z] x, y, or z

[^x] any character but x

. any character but new-line

^x x at the beginning of a line

<y>x x when lex is in start condition y

x$ x at the end of a line

x? optional x

x 0, 1, 2, . . . instances of x

x+ 1, 2, 3, . . . instances of x

x{m,n} m through n occurrences of x

xx|yy either xx or yy

x | the action on x is the action for the next rule

(x) x

x/y x but only if followed by y

{xx} the translation of xx from the definitions section

Expression	Description
`\x`	x, if x is a lex operator
`"xy"`	xy, even if x or y are lex operators (except \)
`[xy]`	x or y
`[x-z]`	x, y, or z
`[^x]`	any character but x
`.`	any character but new-line
`^x`	x at the beginning of a line
`<y>x`	x when lex is in start condition y
`x$`	x at the end of a line
`x?`	optional x
`x`	0, 1, 2, . . . instances of x
`x+`	1, 2, 3, . . . instances of x
`x{m,n}`	m through n occurrences of x
`xx\|yy`	either xx or yy
`x \|`	the action on x is the action for the next rule
`(x)`	x
`x/y`	x but only if followed by y
`{xx}`	the translation of xx from the definitions section