Sets - Sets(3C++)
Sets are the most fundamental structures in all mathematics.
Naturally, there
are many computer applications for sets.
Recognizing this, language designers have
provided sets as built-in types in languages like Pascal and SETL.
Lacking language support,
the C programmer who needs sets is forced to represent them using any of
a variety of available data structures,
including lists, arrays, search trees, and
(for integer sets only) bit vectors.
Unfortunately, the effort needed to implement
sets detracts from the effort devoted to the application per
se. Furthermore, the resulting code is often hard to read and maintain.
For example, unless the original programmer
has left very clear comments (or assertions)
in the code, it may not be obvious to a maintainer
that a particular array is being
used to represent a set; an innocent change
may destroy the invariant property that
no two elements of the array may have the same value,
causing catastrophic program failure.
This memo describes a new library component that allows C++ programmers to
declare and manipulate sets just as if
they were types built into the language.
The component consists of three unordered collection
classes:
As you can see, all three classes are parameterized by the element type,
which we denote here (as in
Set(3C++)
by the Greek letter tau (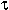 ).
Sets and Bags contain objects of type
).
Sets and Bags contain objects of type 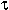 .
The difference between Sets and Bags is that,
while a Set cannot contain more than one object with the same value,
a Bag can contain
multiple instances. Set_of_p's (which we usually call ``pointer sets''),
contain pointers to objects of type
.
The difference between Sets and Bags is that,
while a Set cannot contain more than one object with the same value,
a Bag can contain
multiple instances. Set_of_p's (which we usually call ``pointer sets''),
contain pointers to objects of type 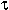 .
Pointer sets
are typically used to keep track of objects
that belong to the client; in fact, such
objects may be pointed to by several pointer sets simultaneously.
The three classes
have nearly identical interfaces.
.
Pointer sets
are typically used to keep track of objects
that belong to the client; in fact, such
objects may be pointed to by several pointer sets simultaneously.
The three classes
have nearly identical interfaces.
The three classes have all the expected algebraic
(for example, intersection, union)
and relational (for example, subset, superset) operations.
We will focus on issues that
are much more likely than these to trip up new users, including:
-
the instantiation procedure, including how to satisfy the requirements
for type parameters
-
how to structure your source
-
how to provide a hash function (needed for Sets and Bags)
-
information about the implementation that will help you make informed
time-space tradeoffs and optimizations such as modifying elements in place.
We do this by presenting three short but complete examples.
Next topic:
A Set example
© 2004 The SCO Group, Inc. All rights reserved.
UnixWare 7 Release 7.1.4 - 27 April 2004
 > -- Sets of objects of type
> -- Sets of objects of type
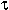
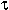 > -- Bags of objects of type
> -- Bags of objects of type
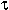
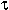 > -- Sets of pointers to
objects of type
> -- Sets of pointers to
objects of type 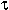
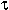 > -- Sets of objects of type
> -- Sets of objects of type
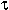
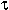 > -- Bags of objects of type
> -- Bags of objects of type
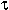
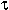 > -- Sets of pointers to
objects of type
> -- Sets of pointers to
objects of type 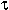
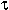 ).
Sets and Bags contain objects of type
).
Sets and Bags contain objects of type 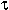 .
The difference between Sets and Bags is that,
while a Set cannot contain more than one object with the same value,
a Bag can contain
multiple instances. Set_of_p's (which we usually call ``pointer sets''),
contain pointers to objects of type
.
The difference between Sets and Bags is that,
while a Set cannot contain more than one object with the same value,
a Bag can contain
multiple instances. Set_of_p's (which we usually call ``pointer sets''),
contain pointers to objects of type 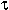 .
Pointer sets
are typically used to keep track of objects
that belong to the client; in fact, such
objects may be pointed to by several pointer sets simultaneously.
The three classes
have nearly identical interfaces.
.
Pointer sets
are typically used to keep track of objects
that belong to the client; in fact, such
objects may be pointed to by several pointer sets simultaneously.
The three classes
have nearly identical interfaces.