|
|
Many programming problems deal with how to represent data items which are related. A good first question to ask is, ``What is the nature of the relation?'' when considering its representation. For instance, do the items relate to each other in only one way, or several? Graphs provide a general purpose data structure for representing problems in which data items may be related simultaneously in as many ways as is required, and a context in which the data can be analyzed via algorithms that inspect and process graph components. Applications for graphs range from scheduling systems, to bills of material, to family trees, to program representations, to communications networks: in fact, every programming problem that relates data items can be represented by a graph (although it may not be the most appropriate choice for some).
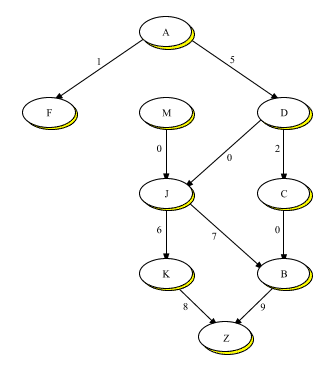
For instance, let's consider a typical programming problem such as representing a manufacturing process. In this paper we'll use graphs to represent the manufacture of a ``widget'', with the component modules of the widget being the data items that are related. Figure 1 pictures one way in which the modules, labeled A, B, etc., might be so related. Where arrows exist, they indicate the direction of the relation, creating an ordered pair of objects related through a directed edge. Thus, modules D and J form such a pair; so do modules M and J. When module D has a directed edge to module J it will mean, in this example, that D must be manufactured before J and is used directly in J's manufacture.

The Manufacture of a Widget
Note that the different modules in Figure 1 are related to each other in different ways: some modules have directed edges to other modules, others not: some modules have such edges to more than one module, and others not.
The manufacturing relation can be easily represented by a graph. Graphs have been the subject of extensive theoretical study and are included in any typical introduction to the data structures used in computer science. Because of their generality, graphs are an excellent choice for a data structure while a problem relation is being refined, and may well be the structure of choice after the relation has been finalized.
In this tutorial we describe the C++ Graph, Vertex, and Edge classes, hereafter also described as ``the Graph classes'' or ``the Graph package'', along with the accompanying Graph Algorithms package. These packages provide the graph data structure and related material, and take care of the associated record-keeping.
We'll first concentrate on using Graph classes with the manufacturing example to understand how to use a directed graph; we'll then discuss the use of an undirected graph as part of the discussion of one of the Graph Algorithms, artic_pts (see the following section, ``What is a Graph?'').
Familiarity with the Set, List, String, and Map components is assumed in the following discussion.